If you are new to building tube amplifiers and are not very familiar with basic electronics and schematic symbols, I would strongly suggest reading the other articles on my site as well as other sites, and purchase either a small kit (like the 30-in-One kit from Radio Shack) and/or books from Radio Shack or your local bookstore on basic electronics so you can be familiar with the basic components and their function in a circuit. The kit will allow you to work with low voltage (read safe) circuits while gaining an understanding of the components involved and the concepts of circuit design. They also familiarize you with the schematic symbols.
Also, as on my home page I offer this warning: Tube circuitry employs dangerously high voltages. Never work on a circuit while it is powered up, except to read voltages and signals with well insulated meter probes. Always wait for the circuit to fully drain before working on it when power is removed. Make up a "bleeder" circuit using a 100K 2 watt resistor with insulated alligator clips at either end (with some wire attached. Use electrical tape to insulate the bare wires) so you can drain power supply capacitors fully, since these can still store some electricity or regain it due to a phenomenon called soakage. Simply clip one end to ground and the other end to the positive terminal of the capacitor, or one end to negative and the other to positive. Voltage levels from 25 volts and up can be lethal. I mean, you can DIE from it. PLEASE be careful.
Also, it is assumed that you read and built the basic tube amplifier power supply circuit so that you can power your first tube amplifier.
Also, you would want to consider whether you want to use a breadboard (the board you get from Radio Shack with all the little holes) or a steel or aluminum chassis or a piece of wooden shelf. I put my SE amp on a piece of 1'x2'x1" shelf. Looks pretty neat and kind of 20's vintage.
Using a steel or aluminum chassis requires some skills in sheet metal work and some power tools. I will use simply a drill and a couple of bits, varying in sizes from 3/16th inch for screws to 1 1/16th inch (one and one sixteenth) for tube socket holes (or whatever the size is you have. Some sockets can be a little bit larger than others). Use the carbide steel bits. Although I would guess that an aluminum chassis would be easiest to drill through, the steel ones will be better for conduction if you desire to use the chassis as a ground. I am fortunate to have an old amplifier with the necessary holes for my experiments.
If you can get or actually have them, you may use parts scrounged from existing amplifiers. Just make note of where the wires on power and audio transformers went so as to connect them properly in your new designs.
Use 1/2 watt resistors except where otherwise noted. New ones would be better and 5% or better (the lower the number the better) is recommended for best results.
Now with all the pleasantries and preliminaries aside, on to designing our first circuit.
A SIMPLE LINE AMPLIFIER CIRCUIT
The first active circuit that just about every student of electronics learns is the simple class A single stage line amplifier. This amplifier takes a small signal and makes it bigger. Ideally it will be an exact representation of the original signal, but larger. Dream on. In the real world there are so many things that cause a changing of the shape of the input signal, known as nonlinearities, that it is virtually impossible to make a simple single stage amplifier that puts out a perfect larger example of the input. These nonlinearities come from the capacitors, to a much smaller but relevant extent resistors, and the active amplification device itself, namely the tube. However, as will be learned in later projects, it is possible to dramatically reduce or compensate for the nonlinearities.
To be honest, though, I used to think that a simple circuit was pure, too. Until a friend of mine tested my amplifier. It had a distortion rating of 3 to 4 percent. That is, 4% of the output signal was distortion. Well, that explanation is not entirely accurate, but it is close enough. Anyway, the amp, to me and my friends, sounds phenomenal, for something so simple and cheap. Oh, by the way it was a solid state amplifier. But go figure. A simple tube amp can also sound phenomenal while producing much distortion. Of course, in this case distortion is relative. This is discussed HERE.
Anyway, the class A ( which means that
the amplifier amplifies the entire wave of the signal) amplifier
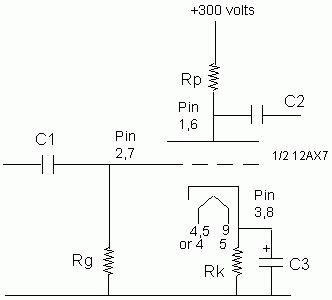
is made with a single tube and a handful of parts. The entire circuit looks
like this:

This circuit can be designed using simple Ohms law to calculate the values of the resistors. The capacitors however require some trigonometry, but the equation is simple enough. Calculating other factors like gain are a little more difficult. But we will go over them here anyway so you the first timers will not be so intimidated the next time someone asks you to calculate the gain of the stage of an amplifier with nothing more than transconductance and plate resistance (HUH!!!???).
A few of the first things we want to understand and consider when desinging a tube amplifier are the maximum plate voltage, the cathode current, the cut off, and the power dissipation.
PLATE VOLTAGE - is the maximum voltage that can be applied to the plate of a tube before the materials start to break down.
CATHODE CURRENT - the maximum current that can be used in a tube before the coating of the cathode starts to boil off causing a decrease in electron emission. The tube gets weak and performance suffers dramatically. Tube life lessens greatly when this limit is met or exceeded.
CUT OFF - Is the negative voltage level of the grid that stops current flow through the tube (effective current flow that is. There is still a very small amount of current flow through the tube at cut off). This can vary from as little as -3 volts to as much as -100 volts. This can be set by a fixed voltage from the power supply, or self bias AKA cathode bias. This is where whatever voltage is set at the cathode, the grid sees a negative version of it. If the cathode has 2 volts on it, the grid will measure -2 volts, relative to the cathode, that is. (Really and truly! It is almost magical!) So if the cathode happens to be directly connected to ground, the grid must be brought minus by a separate minus supply voltage.
POWER DISSIPATION - The maximum amount of power that a tubes plate can withstand before melting down. Or becoming cherry red, anyway. This is not necessarily related to power output.
The above glossary is not necessarily in the order in which we will discuss the design of a circuit, but it is to familiarize you with the first few terms.
To begin with, let's pick a tube to build our amp. Let's use the ever popular 12AX7 high mu twin triode tube. Let's ignore the term "high mu" for now and just say that this tube can amplify a whole lot depending on how we design the circuit.
So we look up the above parameters and the RCA tube manual says 1 watt dissipation, 500 volts plate voltage, -50 volts grid voltage, and 8 milliamps current. Remember, these are maximums. There is no way that this tube can work for long with 500 volts and 8 milliamps, because this would put 4 watts on the plate (voltage times current equals power). Meltdown followed by implosion might be the result (that is, the glass will squeeze itself from the pressure of the atmosphere, having a vacuum within, while the glass itself is soft because of the excessive heat of the plate). I have seldom seen an amplifier desinged to have a -50 volts at the grid. It is usually for class C or high power audio or radio transmitter tubes.
These amounts are maximums for each parameter individually, not all at once. So to consider the tube's power rating of 1 watt, we would want to do something like use 300 volts for the power supply, where the plate actually gets a constant voltage of about 145 volts. Then take that 145 volts and figure out the current level to keep the tube idling at about half of its power level, or 0.5 watts. So we use the power equation P=IE (Power equals Current times Voltage, as represented by the I and E respectively) and juggle it aroung a bit to solve for X, which is the current we want. So I=P/E or I=0.5/145 or 3.4 milliamps. This is actualy kind of high for a current rating, but according to some charts, we can get a low distortion and noise rating with this current level. Personally, I would use no more than 2 milliamps because I want to have some longevity from the tube. (A tube can last up to thirty years of service. I have antique radios that have original tubes from the twenties that still work very well. That's more than sixty five years.)
An interesting side note is that the plate sees the most power dissipation when at idle. If we were to do some slightly complicated math on the power output of the tube as a whole, we will find that at peak (either peak) the power dissipated will be quite low. For example, if I make the tube go to B+, then that means that the tube is not conducting. If it is not conducting then there is no current flowing through it. If there is no current flowing, there is no power dissipated, due to the power formula P=IE. Conversely, if the current is the most the tube will allow through, then the voltage at the plate will be whatever the cathode resistor plus the tube itself will drop (theoreticaly it should be zero, assuming dynamic conditions anda bypass capacitor), and the power will be that times the current. If theoretically current is about 3.5 milliamps and the voltage at the plate is about 5 volts, then the power being dissipated is only about 17.5 milliwatts. Remember, we are idling at .5 watts, or 500 milliwatts! So power out of the amp is really lower than what the tube is dissipating. This is actually a problem with class A operation, but for low power small signal applications, it is an acceptable efficiency problem. Class A amps are generally about 20% efficient. That is 20% of the total dissipation is actually seen as signal power.
For the sake of simplicity in designing our amp, let's use 2 milliamps. So now we want to calculate the resistor for the cathode first. We want the bias on the tube to be at a level where at full volume the tube can take a line level signal, which is 0.5 volts standard. CD players can put out up to 2 volts. These are RMS levels. RMS stands for Root Mean Squared. I never bothered to memorize what that was derived from because in electronics I reallly don't care (my personal opinion. I leave alot of facts in the textbooks). Electricians might be more keen to this term and its significance, but for electronics we use it often enough to need to know how to calculate for it. The calculation we will use, though, is for a pure AC sine wave only. Complex waves have a variety of formulas for RMS.
We could set the tube's bias for 0.5 volts, but this would be pushing things a bit. For one thing, the RMS means that the 0.5 volts is not really the full voltage swing. What we need to do to find full voltage swing is to multiply the RMS level by 1.414, then double it. RMS is calculated from half of a wave times 0.707. So the full swing of a 0.5 volt signal is (0.5X1.414)x2 or (coincidentally. Or maybe not) 1.414 volts peak to peak, or full signal.
Putting the bias at half of this may accomodate the full swing, but this can still be too close for comfort. So we choose 2 volts, just to make sure the signal doesn't cause the tube to go beyond full swing in either direction. What happens then would be what is called clipping. This is a form of distortion that makes the dreaded odd order harmonics. So we set the bias at two volts so the signal can swing a full four volts peak to peak, or 1.414 volts RMS. For CD input we usually use an attenuator (volume control) anyway, so we needn't worry too much about that. Besides, even the most aggresive classical music doesn't reach this level much if at all because the recordings seem to usually be lower in volume than popular music (this is an observation. I never measured the transients).
So for 2 volts at the cathode with a current of 2 milliamps we calculate, using Ohm's law, a resistor value of 2/0.002 or 1000 Ohms. 1K for short.
Now for the plate resistor. We want to calculate this for a full voltage swing at the plate before clipping. So we want to get about half of the power supply voltage at the plate. But wait, what about the resistor at the cathode? Yes, let's consider the voltage drop across that. So we merely take away that voltage from the power supply voltage and come up with 298 volts. But there is also some voltage drop across the tube. I wouldn't worry too much about that because by the time a signal can make the tube go that far the input is already severely distorted at the cathode. Imagine this, to make the tube swing the full 298 volts, I would require an amplification factor of... well let's calculate it!
298/2X.707=105.343
Gain=Vout/Vin=105.343/0.5=210
A whopping gain of 210! The tube has an inherent amplification factor, called mu, of 100! The circuit we are designing may only have an actual gain of 20 or 30. So we may never clip this thing. (So much for the so called squishing effect or soft clipping of tubes. At least for the first tube. Subject for another discussion). Another way to look at this is assuming a gain of thirty, the required input voltage to clip the output would need to be 105/30, or 3.5 volts RMS, or a peak to peak signal of 10 volts. If we can stand such a large volume like that, then we would be deaf before long and the sound quality of the amp wouldn't mean anything anymore anyway.
OK so we want a plate voltage of around 149. At two milliamps that would require a resistor of about 149/0.002 or 74.5 k ohms. I have seen 68K or 82K. Rarely 75K, but they might be gotten from some supply houses special order, if not actually in stock. So we select one close to that value. 68K seems fair since they are both equally distant from 75K, and the lower value would be better considering that it may allow for the voltage drop across the tube.
We now have the values for the most important part of the amplifier, the bias setting. The grid resistor, or the one from grid to ground, is determined by (in my mind, anyway) two factors. The first is the value of the impedance of the previous stage, or input source. Typical impedance of some sources is about 47 Kilohms. In some instances it is as high as 100 Kilohms. In order to minimize the load on the source, it is a rule of thumb to make the input impedance about ten times the size of the source. This means that the output of the source might actually be 1/10th the recommendations of the manufacturer. This is why some circuits use a resistor from the input to ground before the selector switch and the volume control to match this "requirement".
So we pick 470 K as our grid resistor. This allows us to use a smaller value input capacitor. What does this signify? Who knows. But we can avoid using electrolytics and use higher quality poly or metal film or mica capacitors. Also, the main reason for using such a high value resistor is because, as we will see later, this resistor factors in to the equation for calculating gain from the previous stage in an amplifier.
Now, let's calculate the value of input capacitor. We want the amp to go as low as we can hear. I have recently read that the lowest frequency people can hear is about 15 hertz (although speakers seldom really produce lower than 30). So let's take that value and determine the reactance of the capacitor for that frequency. Using the above guideline of a 10:1 ratio, we want the reactance of the capacitor at 15 hertz to be 1/10th the grid resistor. So for 15 hertz, our unknown capacitor should have a reactance of 47K. The formula for this is:
Xc=1/[(2)x(Pi)x(F)x(C)]
Where:
Xc is the capacitive reactance
Pi=3.14159
F=15 Hertz
C=capacitor value.
However we need to know the capacitor value, so we therefore need to rearrange the formula to solve for C.
C=1/[(2)x(Pi)x(F)x(Xc)]=1/(6.28318)x15x47 000)=1/(4429645.641562)=0.00000022575...
Well, we'll dispense with the overexaggerated accuracy and just say 0.22 microfarads. It is not necessary to be more accurate than that. Calculating down to the nearest tenth or hundredth is sufficient. Do not over do the accuracy because no one is going to make the components for that level. Unless you are willing to pay about $300 bucks for a capacitor. $600 for a hammer. $1 000 for a toilet seat. ;-)
0.22 microfarads just happens to be an industry standard value so you can find it anywhere. A low voltage variety will do for the input because there is barely any voltage there, and likely none (DC) coming from the previous stage except for up to 2 volts AC signal. If one wants to be on the safe side though, choose one of at least the power supply value. Since we are designing for high voltage tube equipment, lets make all of our caps 450 volts or more. They may cost a bit more than the lower voltage ones, but this may come in handy if you want to put a stage of amplification before this one. Then one can merely use a single capacitor of the high voltage value to connect the plate of one to the grid of the other.
The output capacitor on the other hand sees at least 149 volts at one side, so use a capacitor of at least 350 volts. To calculate this one, use the same formula as above, but consider the impedance of the next stage. Assume about five to ten times the output impedance of the output, which we will calculate later. For all intents and purposes we will say about half of the plate resistor (the 68K), or about 34 K (I get this value from dividing the plate resistor by the plate resistance and cathode resistor). Multiply this by ten and this would be the recommended impedance of the next stage. We can then use this (the 34 K) as the reactance value for the output capacitor. Looks like it will be a little more than 0.22 microfarads. Use 0.33 microfarads, also very popular.
So, now we have a mostly complete and operational amplifier ( that is a working amplifier, not to be confused with an op-amp). I say almost complete because there is one capacitor that we have not yet calculated for, the cathode resistor bypass capacitor C3. This will need some discussion before we decide to use it and calculate for it.
But first:
CALCULATING GAIN
Now comes the complicated part. Gain calculation comes in a variety of flavors. The simplest one is Vout/Vin. This is so intuitive so as to be ridiculous. It says that we can calculate the gain of an amplifier by measuring its output voltage for a given input voltage and getting the ratio. Duh! But this requires that we have a working amp and some test equipment. This is no real big deal if we can get the equipment. If we don't have the right amount of gain we can experiment to improve it.
But wouldn't it be real cool if we could figure it out for ourselves and be right? In the words of the immortal Jerome "Curly" Howard "Soit'n'ly! Nyuk, Nyuk, Nyuk!". Lets see how.
There are a couple of other parameters for tubes that we can use to our advantage. They are the amplification factor or mu, transconductance, and cathode resistance.
MU - The amplification factor based on the plate resistance divided by the cathode resistance, which is calculated by the inverse of the transconductance. In other words, for the 12AX7 the amplification factor is said to be 100. For a transconductance of 1600 microsiemens the cathode resistance is 1/0.0016 or 625 ohms. The plate rsistance is advertised as being 62.5 K ohms (all at a certain operating voltage and current). 62500/625 is 100.
TRANSCONDUCTANCE - is the rate of change of output current for input voltage. It is represented by the equation Gm= dIout/dVin. That is, trandconductance is the ratio of a change of current out (dee-eye-out) for the change of voltage in (dee-Vee-in. The dee is really a delta, which means change). So a transconductance of 1600 microsiemens (the old way of saying it is micromho. Mho is the opposite of Ohm, like conductance is the opposite of resistance) is like saying that for each volt input the output moves 1.6 milliamps. How did I arrive at this? Algebra. I rearranged the equation so that dIout=Gm*dVin, or output current change is equal to transconductance (Gm) times change in voltage. If I had a voltage change in of 1 volt and multiplied 0.0016 by 1, then the resultant output is 1.6 milliamps. Heck, that one volt will bring our tube close to saturation, or full on.
CATHODE RESISTANCE - has been answered by the MU portion. However, there is a thing known as effective resistance. This means that the resistances, both plate and cathode resistances, need to be considered in connection with the other resistances in the circuit. In other words, the resistance of the following stage is calculated in parallel with the plate resistance and plate resistor.
Now, gain can be measured as the ratio of output resistance to cathode resistance also. This ratio should theoretically be equal to the voltage out to voltage in ratio. This is because the signal at the cathode is just a little bit less than the signal at the grid. The signal at the cathode resistor is lower because the cathode resistance and the cathode resistor are in series, so they act as a voltage divider.
The gain can also be expressed as Vp/Vk. Since this is a ratio, then it would stand to reason that the resistances can also maintain this ratio, since resistance is related to voltage as per Ohms law, and currents remain equal for the plate circuit as for the cathode circuit (remember, earlier we calculated the plate resistor based on the current we chose to calculate the cathode resistor). So, what is the gain of our stage as it stands without the bypass capacitor? Let's calculate using this equation and find the resistance ratio A.K.A. gain:
Gain= Rp||rp||Rload/rk+Rk
Where
Rp is the external plate resistor
rp is internal plate resistance
Rload is the resistance of the next stage
(All of the above are paralleled as indicated by {||}
using the formula 1/[(1/r1)+(1/r2)+(1/r3)+...])
rk is the internal cathode resistance
Rk is the cathode resistor
So for our example above, assuming a 330k load from the next stage, the resulting actual gain is:
1/(1/62 500)+(1/68 000)+(1/330 000) = 29 673 ohms.
Effective cathode resistance is 625+1 000 = 1 625
Gain=29 673/1 625 = 18
The gain of this stage as it is with no bypass capacitor is 18! That low??? Yup.
THE CATHODE BYPASS CAPACITOR
The purpose of the cathode bypass capacitor is to eliminate the effect of the resistor to oppose the flow of AC. So this resistor is a form of negative feedback, also known as degenerative feedback, since across it is an exact, albeit reduced a little, replica of the input, with some of the distortions of the tube included. This signal combines with the input signal in the tube to make for less output and less distortion. It does this because at the plate, a signal coming into the grid is inverted. But a signal coming into the cathode is not inverted. So the combination is like on a number line, where a positive number plus a minus smaller number add to a smaller plus number (5+[-3]=+2). The bypass cap makes the effective cathode resistance 625 instead of 1625. So the result there would be a gain of 29673/625 or 47.
If you want that much gain, and wish to add this capacitor, then we need to calculate for it the same way as for the other capacitors, with the 10% rule. So for a low frequency of 20, we use the capacitive reactance formula and plug 20 and 100 (10% of 1000) to get a capacitor value of 79 microfarads. There are none easily available so 100 microfarads will do. The voltage of this one can be 10 volts, because the biggest voltage the cathode might ever see is -4 volts. But get a 25 volt one, just to be on the safe side.
Seldom if ever does the tube see a gain of 100. But it is nice to have around, because we can make some rather sensitive circuits with high gain by using more tubes. It would use less than if we used tubes with a MU of 20 like some tubes can be. In some circuits the gain of these high gain tubes can actually come close to 100, but we aren't too concerned with that much gain in audio because the benefits come with some caveats. Two are increased noise and microphonics.
You may want to add a volume control to this amp. Doing so is very simple. Use one of at least 100K. It must be an audio taper type. This means that as you turn the shaft clockwise, the resistance changes logarithmically, not linearly. In other words it gradually changes. A linear potentiometer changes more abruptly. This is because we hear logarithmically.
The input signal will go across the outer pins of the volume control, and the center of the potentiometer (A.K.A. volume control. POT for short) and the ground side will go to the input of our amplifier. Generally speaking, looking at the pot from the top (with the shaft pointing towards you and the pins pointing down), the ground, or common, connection will go to the pin on the left, the center goes to the amp input, and the signal goes to the right pin.
Once you make your first line amp and
connect it to a power amp and plug in your favorite CD player or tuner
and are comfortable with its performence and your ability and skill in
designing an amp, we can go on to the My Second
Tube Amplifier.
Back Home
Back to Projects Page